Learning Graph-based Disentangled Representations for Next POI Recommendation
Learning Graph-based Disentangled Representations for Next POI Recommendation
1. Introduction
首先简单理解disentangled representation(解离化表示)的相关概念:解离化旨在对数据变化因素进行建模,是指将embedding拆分成不同维度,使得每一个维度可以代表一种语义。
存在问题
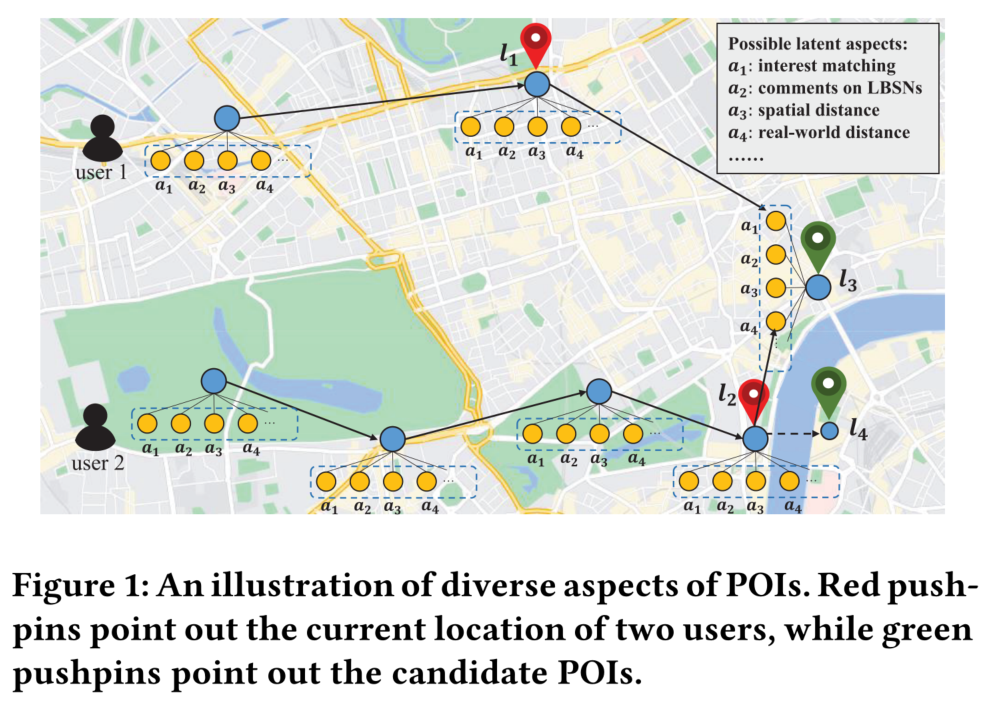
(1)第一,POI对用户转变的各种潜在影响没有得到有效的分解。
例如用户u1去l3的主要原因是个人偏好,尽管l3距离他当前的位置l1较远。另外一方面,用户u2更关注l3本身的作用(例如为餐厅),并且更关心距离。然而现有方法大多专注于黑盒模型的训练,将这些因素忽略了。
(2)其次,在以往的大多数方法中,POI 的基于距离的影响也过于简化了。
例如l3和l4作用相同,l4甚至距离ll2更近,但或许由于物理因素的影响(例如河流),用户还是选择了l3。因此,POI 之间的距离影响可能包含多种因素,仅仅基于距离的表示并不合理。
论文专注于对 POI 进行更好地表征,提出了一个新的 Disentangled Representation-enhanced Attention Network (DRAN),将 POI 表示分解为多个独立的分量;提出了 Disentangled Graph Convolution Network (DGCN) 学习 POI 表征,并对 self-Attention 进行拓展,以及建模用户偏好。
2. Contributions
- 明确了 POI 包含的多方面因素并进行分解,并提出 DGCN 进行实现;
- 提出 DRAN,充分利用 POI 全局信息并学习用户的动态偏好。
3. Preliminaries
3.1 problem formulation

3.2 Graph Convolution
图卷积运算可以看作是一种节点表示学习方法,它通过聚合邻居节点的信息来更新节点表示。

3.3 Disentangled Representation

4. Proposed Method
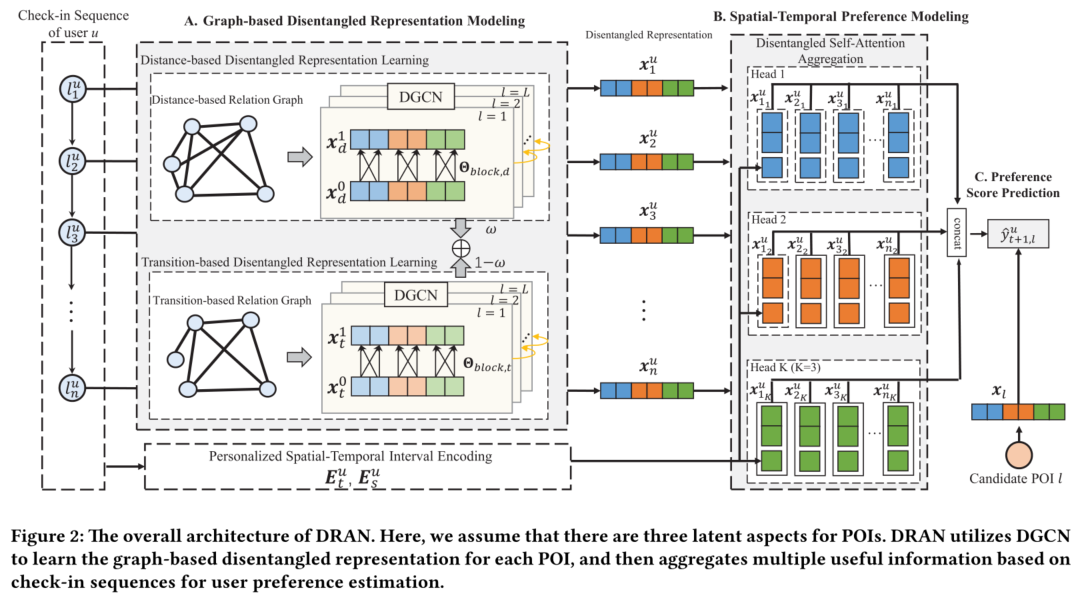
由三个关键组件组成:
(1)基于图的解纠缠表示建模模块(图2中的A部分),该模块利用新提出的DGCN层学习POIs的解纠缠表示;
(2)用户时空偏好建模模块(图2中B部分),该模块集成相关时空信息,对用户历史签到序列进行建模;
(3)预测与优化模块(图2中的C部分),该模块估计用户偏好并优化所有可训练参数。
4.1 Graph-based Disentangled Representation Modeling
4.1.1 POI Relation Graph Construction
为了更好地学习 POI 的内在特征,论文提出了两个 POI 全局关系图来更好地进行特征学习:距离矩阵和转移矩阵。

4.1.2 Disentangled Representation Propagation
论文希望利用 GCN 从 POI 关系矩阵中学习其分解表示,同时保持不同部分的独立。计算如下:

$x_m$的每个维度与其他维度都具有非常强的关联,这限制了 POI 分解表示的能力。因此,论文只将同个 POI 内的不同维度相互关联:

4.1.3 Representation Aggregation
在 POI 关系矩阵上应用了L层的 DGCN 之后,使用聚合策略将多层表示进行聚合,论文中直接相加:

在对两个 POI 关系矩阵进行适当表示,以模拟K个部分的分解表示之后,一个简单的想法是这将两个部分串联起来最为最终的表示。但是论文考虑到两个原因并没有这么做:
- 需要引入超参数来平衡两者之间的比例,可能无法保持不同类型的影响;
- POI 本身就包含不同因素的影响,只表示为一种特殊类型可能会限制其能力。
4.2 User Spatial-Temporal Preference Modeling

4.2.1 Personalized Spatial-Temporal Interval Encoding
通常来说,用户对 POI 的偏好很大程度上受空间距离的限制,用户更愿意访问附近的 POI。此外,用户的历史轨迹也在一定程度上反映出了用户偏好。因此论文明确了 POI 之间的时间空间关系进行建模,时间间隔矩阵和空间间隔矩阵表示如下:
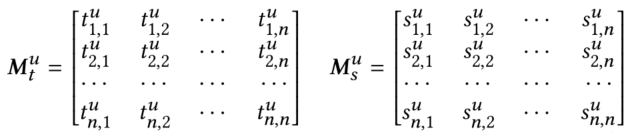
4.2.2 Disentangled Self-Attention Aggregation
为了捕获签到序列的多层次规律,论文提出了一种拓展的 self-attention。具体来说,将每个部分分为一个单独的注意力头:
4.2.3 User Preference Estimation
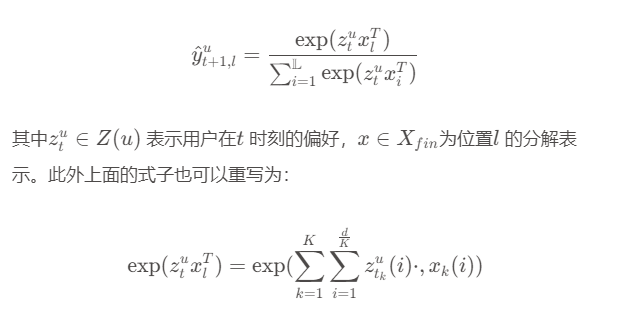
4.3 Model Optimization
使用交叉熵损失函数计算损失:
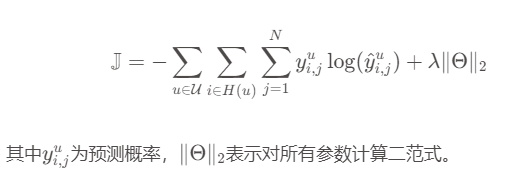
5. Experiment
5.1 Experimental Setup
5.1.1 Datasets

5.1.2 Baselines
5.1.3 Evaluation Metrics
5.1.4 Parameter Settings
5.2 Performance Comparison
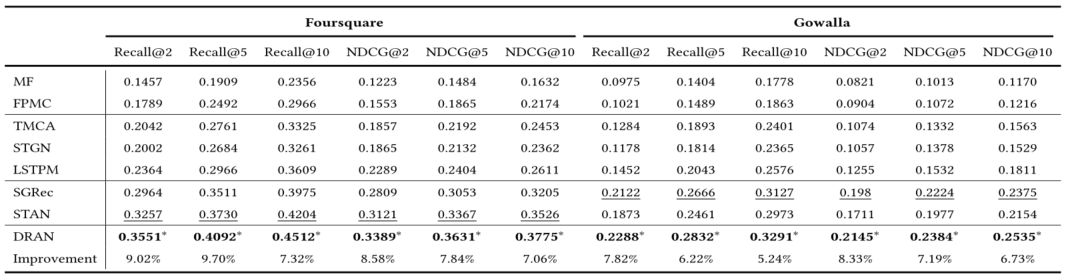
5.3 Ablation Study

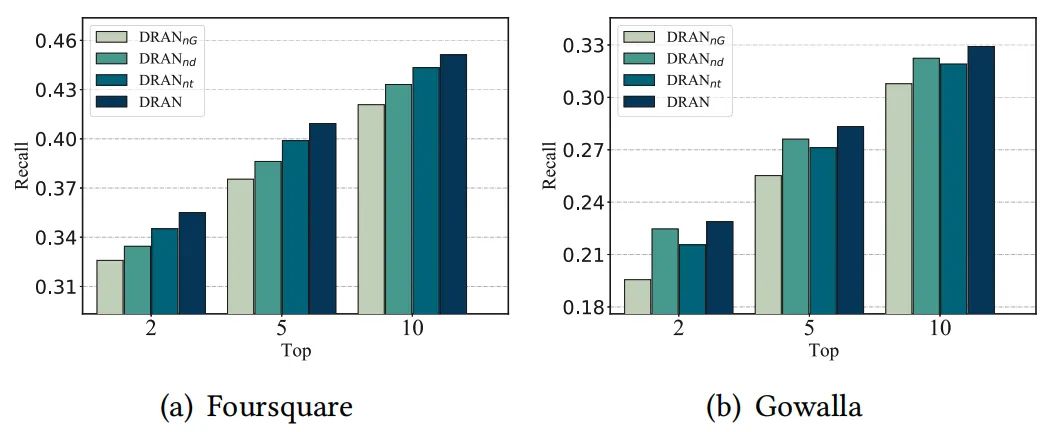
5.4 Hyperparameter Study
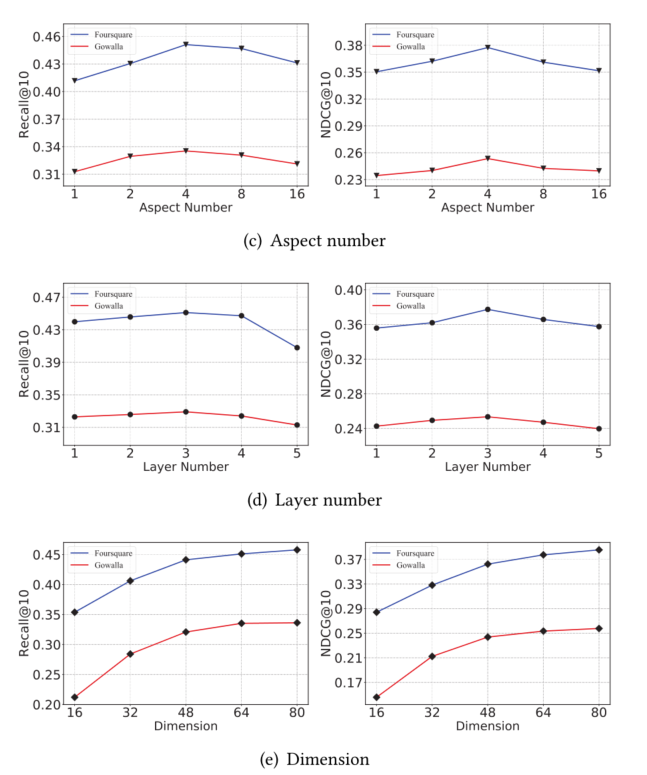
5.4.1
5.4.2
5.4.3
